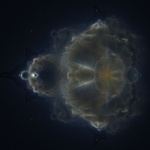
What’s the Mandelbrot set?
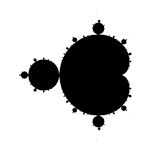
The Mandelbrot set is a fractal. You can find more information with this Wikipedia article on the Mandelbrot set, but put simply: The Mandelbrot set is the result of running the formula zn+1 = zn2 + c for each point in a range. For every point the formula is iterated many times, if the absolute value of z increase beyond a threshold, it’s not inside the set, otherwise it is.
That’s the basic idea, at least. Different ways of viewing the data that this simple formula generates are possible. For instance, instead of simply using black and white, if each pixel is colored from a palette of colors based off the number of times it takes for z to reach the threshold value, you end up with the color image shown here.
You can take this coloring idea a step further and pick the colors from a palette of smoothly changing colors, and smooth the change further based on how far the value escapes. That’s what I’ve done with the “Mandelbrot” view here.
The Buddhabrot
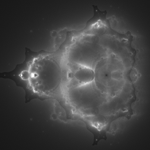
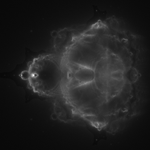
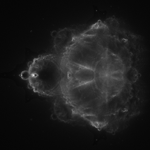
As I said, there are different ways to visualize the data generated by running the formula. Instead of coloring a pixel based off how fast the formula reaches a threshold, keep track of each pixel the formula touches as it iterates. For each run of the formula that results in a point outside the set, increase the color of each pixel touched by z for each iteration a bit. This produces the Buddhabrot image.
This is a simple gray scale image. One of the interesting things to note is that the image differs depending on how many iterations you’re willing to calculate.
Coloring the Buddhabrot
The most common way to color the Buddhabort is to render three separate images at different iteration values. This produces subtly different images. Then each image can be used as one of the red, green, or blue channels to create a false color image, and use a histogram equalization function to control brightness. This is the similar to the technique used to produce false color astronomy images from different wavelengths of light. Indeed, this is the basic idea that Melinda Green used to develop her famous view of the Buddhabrot. You can read more about it on her website. Many thanks to her for help on rendering the “Normal” view presented here on the large scale render.
The alternative method I’ve used for the large scale map, called “Escape Coloring” here is to use the escape location to influence the color. Basically, one can add up the value for c for each pixel the iteration touches. When that’s done, you can use the complex argument of the final value for each pixel to pick a color on a spectrum, and the absolute value to control the intensity.
And on top of that, for the large scale map I’ve used a slightly muted map of colors compared to the range of colors produced by a traditional HSV algorithm to adjust for perceptual brightness, and just because I like the way it looks.
Wallpapers
Here are some wallpapers you can download. Also, you can create your own wallpaper using the “Wallpaper of current view” link on the main page to create an image of any view you select.
Buddhabrot: Escape Direction Coloring
Apple iPad, Apple iPhone, Dual Monitors, Fullscreen 4:3, Fullscreen 5:4, Google Android, Microsoft Surface, Portrait Orientation, Triple Monitors, Widescreen, Widescreen 16:10, Widescreen 16:9, Widescreen 21:9, Widescreen 24:10
Buddhabrot: Escape Traditional Coloring
Apple iPad, Apple iPhone, Dual Monitors, Fullscreen 4:3, Fullscreen 5:4, Google Android, Microsoft Surface, Portrait Orientation, Triple Monitors, Widescreen, Widescreen 16:10, Widescreen 16:9, Widescreen 21:9, Widescreen 24:10
Some parting comments
By far the hardest part of drawing the 1,048,576 x 1,048,576 image is the sheer memory pressure. Because when rendering the Buddhabrot each pixel can touch just about any other pixel in the final image, it’s best to keep the entire array of pixels in memory. And there’s a severe performance impact each if that memory buffer spills over to disk. For smaller images, or even some larger images with only a height map, this isn’t an insurmountable challenge. For this image, however, it would require 24tb of RAM just for the image data, not to mention other smaller uses of memory ((8 bytes for the height map + 16 for the complex value) * (1,048,576 pixels wide * 1,048,576 tall) = 26,388,279,066,624 bytes). Since I don’t yet have 24tb of RAM to spare, I ended up rendering the entire image several times, but only keeping a small window of the final result in memory. After each pass, the results were saved, and a final worker was responsible for combining the results using disk back memory buffers. All told it was several months of computer time spent rendering, spread over a few computers, each with more CPUs and memory than an average home computer.
From there it was a relatively simple matter of splitting up the logical large image into 89,478,485 individual 256 x 256 tiles for the various resolutions needed for each of the three scalable maps. A small program was used to piece together the tiles into larger images for the wallpapers and the two zoom videos:
And I’ll close out with some stats:
- For the “Colorful” Buddhabrot set with escape values coloring the set:
- Source data size: 87,960,930,226,176 bytes
- Size of all tiles here: 2,180,938,396,992 bytes
- Iterations: 500,000
- For the “Normal” Buddhabrot set with three renders:
- Source data size: 13,194,139,534,336 bytes
- Size of all tiles here: 3,439,165,408,296 bytes
- Iterations: 10,000 for red, 500 for green, 100 for blue
- For the Mandelbrot set:
- Source data size: 3,298,534,884,352 bytes
- Size of all tiles here: 60,802,213,501 bytes
- Iterations: 500,000
-- Scott Seligman
Page last updated: 2019/2/21 7:53 AM